StockRanks | A Quick Look At The Best Targets To Use For QVM Ranks For Different Risk Appetites - Is Bigger Always Better?

4th Feb '20 by Nick Ray

8 comments 1463 reads

Introduction

There have been a few comments about how well (or how badly) the various stock ranks work in practice. So this post looks at their performance and makes some observations about how to get the best from them in the conclusions.

[Caveat - the data in this post is based on stocks with a market cap greater than £75m and values from 2016 to the present.]

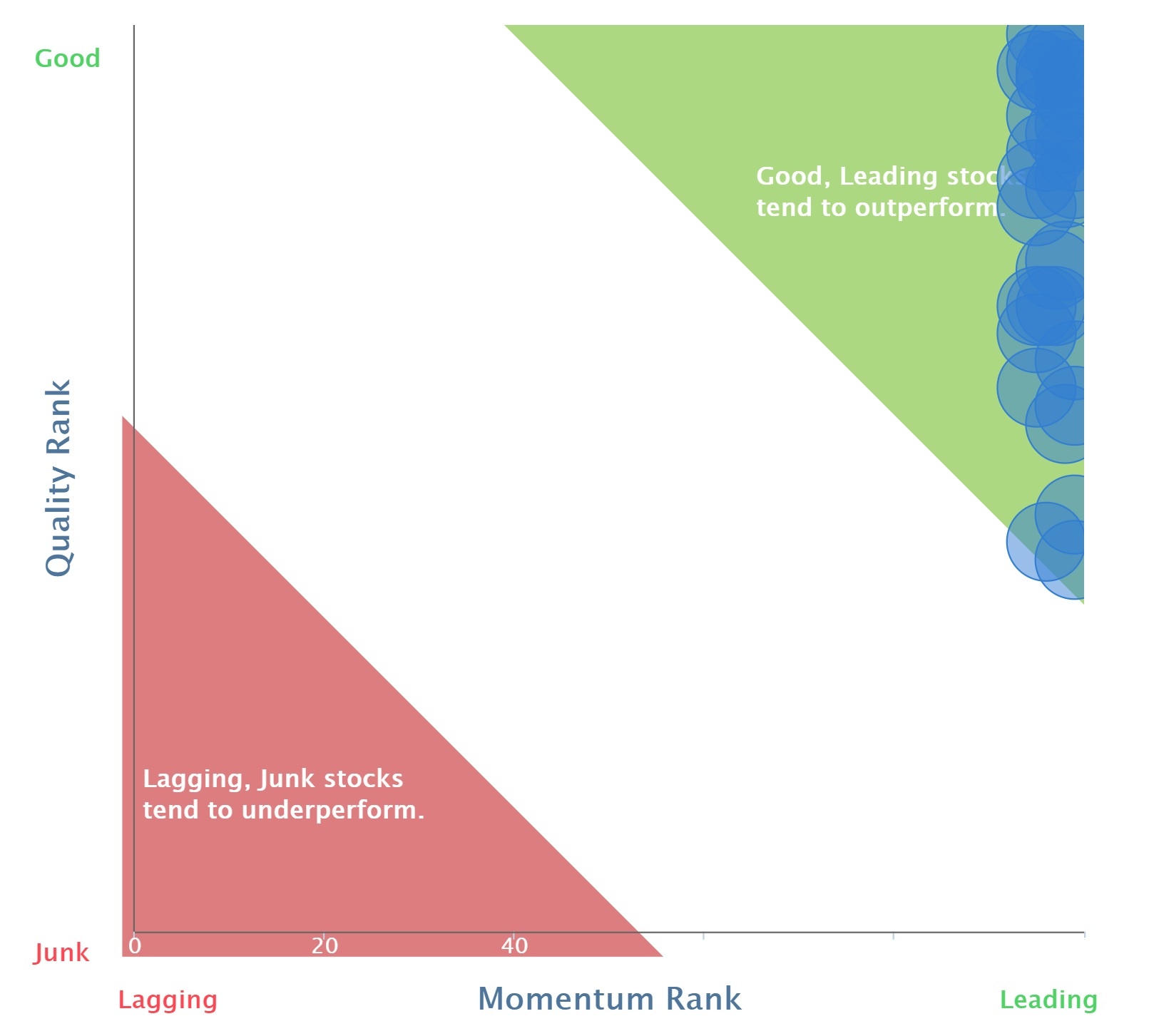
The basic premise behind the Quality Rank, Value Rank and Momentum Rank is that the bigger the rank the better. But what does "better" mean and is it even true that bigger means better? Here are some guidelines on how to use these metrics depending on your risk appetite.

First question though: what is a "rank"? In statistics, a rank is just the position of a value when all the values in the data set are sorted. If this position is converted into a percentage position along the sort it is called a percentile rank which is what each of the Stockopedia Ranks are.

Each of Q V M is a ranked average of a set of ranked metrics. The numbers are determined by a mathematical formula with no subjective aspect (after the initial decision about which metrics to combine.) So we can ignore any human-implied meaning from their very suggestive names and dispassionately look at what they can tell us about capital returns for the following year.

We will ask the question: what is the probability that a given Q V M value (in range 0-100) will result in a yearly return greater than some target? (which we will also express as a percentile rank of possible yearly returns.)

50% quantile yearly returns

Let's start with the simple case of the 50% percentile. So we are asking for the probability that we can get a return better than the median. Approximately: can we "beat" the market (assuming the market return is close to the median return)?

Here are the results for each of Q V M expressed as a likelihood ratio. Without going into detail, the bigger the likelihood ratio the better, and values above 1 indicate doing better than chance (picking stocks at random). The '1' line is drawn in grey on all the plots for ease of reading.

[There is a technical issue here. When you compare the likelihood ratios for say…

Unlock with Email

Unlock with Google

Already have an account?
Login here

WarrantStar

4th Feb '20

Thanks Nick. I will build a screen around your conclusions. Then I will form a judgement as to whether or not I should invest in any of them. It's likely to come up with with a lot of results so the a key feature will be what I should use to sort the table. My initial thought on this is to use the overall Stockrank,

William K

5th Feb '20

Thanks Nick. A fascinating and counterintuitive article. My take on it is that:

High value - the stocks are cheap, but for a good reason

High momentum - the crowd is usually right (the trend is your friend)

High quality - shares are overpriced because many investors focus on EPS, which can be easily manipulated by buy-backs and creative accounting.

It would seem that Stock Rank and QM are the more useful markers for aiming at returns above the median, or avoiding large losses.

Thanks again Nick. Plenty to reflect upon.

iwright7

A truly insightful analysis of the probability of a group of stocks winning. I personally really like High QM style investing and rate Q and M as important components of market beating returns.

In your analysis High Momentum has done particularly well, so if using Momentum as the basis for stock picking it becomes important to take account of aspects like: Nearness to 52 Wk High, 3 month %RS, Broker Upgrades and % Earnings Surprises, (most of which are components of the M Rank). Ed has said many times that a High M Rank was designed to be predictive for out-performance and so this has turned out to be.

Another Momentum aspect that is rarely talked about, but may be as important as the other Momentum factors is insider dealing by corporate individuals who buy because they have privileged information about future company success. The effect of insider trading is impossible to calculate or to screen for except that their actions manifest again as; “the trend is your friend”. I do sometimes wonder when buying a high momentum stock whether I am joining the insider dealing club.

When combining High Q with High M you note that… Even for a stock with a Q>80 or M>90 the likelihood ratio is not huge. It is the equivalent of moving the probability from 50% to about 64% in the "50% quantile" case.

64% likelihood odds look excellent to me and are an outcome that many fund managers fail to achieve.

An excellent piece of research. Ian

pka

7th Feb '20

This is a very interesting article and piece of research. However I think one has to be a bit cautious about acting on its conclusions. It uses the terms probabilities and likelihoods, but I would suggest the values they refer to are really historical frequencies of occurrence based on just four years of statistical data over a period when stock market conditions have been relatively benign. The relative abilities of the various StockRanks to predict future statistical performances of portfolios might be very different in the future to what they were over the last four years, particularly if there is a major bear market.

finebone

A very interesting analysis that might explain some of the 'anomalies' noted in my comments on 20/1/20 in response to the latest NAPS article:

"Thanks for drawing my attention to this article which referred to Annie Duke. It led me to some very interesting lectures by her on YouTube to both investors and poker players on decision making under conditions of uncertainty.

However, going back to the changes to the NAPS portfolio this year, the best evidence on this site on UK factor investing are the charts of performance of the Stockopedia StockRanks since their launch in 2013.

These confirm that QVM has indeed performed best, although not far ahead of VM and QM eg

> 10M market cap, rebalanced quarterly, to week from 13/1/20:

Stocks with QVM of 90-100: + 176.75%
Stocks with VM of 90-100: + 169.76%
Stocks with QM of 90-100: + 167.79%

Moreover, with a few minor exceptions, in all these cases, the worse the decile score the worse the performance.

However, stocks with QV of 90-100 have “only” risen 86.10% over this almost 7 year period. Moreover, this was beaten by stocks with QV of 70-80 (+93.94%) and stocks with QV of 30-40 did rather better than the score would suggest.

This is reflected in the scores for the individual factors since, although the best performing Value stocks have scores of 90-100 (+65.67%), the second best are those with scores of only 30-40 followed by several others which seem out of place eg 70-80 is in 6th place!

For comparison, stocks with Q alone of 90-100 gained 126.76% and stocks with M alone gained 166.02% and the usual pattern of worse scoring stocks usually performing worse is re-established.

Hope you are still with me but before I pose a question, I will give the top decile figures more representative of the NAPS portfolio ie > 50M market cap, rebalanced yearly:

QVM +144.63%

QV + 94.26%
VM +129.28%
QM +141.75%

V + 77.54%
Q +111.38%
M +132.83%

In all these cases, the best decile contains the stocks with scores of 90-100, although again there are some anomalies with QV and V stocks. Third best performing decile for QV stocks is 40-50 and 80-90 scoring stocks are 5th. Second best performing decile of V stocks is 30-40 and 80-90 scoring stocks are 7th!

All this makes me wonder if there is some error in the Value data, or the Value algorithm is not accurately enough reflecting value and this is having a knock on effect on the QV and QVM scores.
Or have we just been in unusual market conditions for value? Not sure why it does not seem to be affecting VM though. Over to you, Ed!

PS This is a question, not a criticism, QVM still best performing and comfortably beating the FTSE-A (as are QV and V) over almost 7 years. Thanks for all the wonderful information!"

Bearing in mind that most of us are probably looking for significantly better returns than the market (to justify the extra trading costs and time involved compared to buying a passive market tracker), this analysis suggests that it is a lot trickier than simply selecting stocks with high QVM scores, albeit highly diversified in terms of sector, size and risk rating.

If I am reading this analysis correctly, it would have been better, at least over the last 3-4 years with stocks with a market cap over £75m, to have selected stocks with:

1) M scores as high as possible, preferably over 95

2) Q scores over 80 but not to have worried too much as long as the Q scores remained over 40.

3) V scores anywhere between 20 and 80 for a peaceful life or V less than 15 if you liked excitement.

I will try to check how large a QVM score these criteria will allow but, in the meantime, any comments?

It turns out that nearly all UK stocks that, at present, fit the peaceful life criteria have QVM scores above 80. This includes some with Q scores less than 80- only a few with low V scores too have QVM scores of 64-72. So maybe simply picking stocks with high QVM scores would have been near to optimum over the last 3-4 years after all!

They are also pretty diversified in terms of size (though only a handful are microcaps) and risk rating and all are Super Stocks, High Flyers or Neutral style. However, five sectors would have no or only one stock to pick from unless the M score requirement is relaxed to 90 or over and/or dual listed stocks are allowed.

With these provisos, it would be perfectly possible to pick a pretty diversified portfolio of 20 - 30 UK stocks based on these criteria. Will that be better over the next 3-4 year than simply picking high QVM stocks? Who knows?!

8th Feb '20

I have run the Peaceful Life screen using criteria 1-3 using >£50M Mrk Cap with the Q set at >80, or >40. At Q >80 I get 17 selections, whilst at Q> 40 I get 30 companies. Naturally at Q>80 and M >95 we get very high QM scoring shares, but at Q>40 we get more of a QM spread.

M>95, Q>40, V 20-80 and greater £50M Mrk Cap - 30 Companies

Viewed visually dropping to Q >40 produces a neat cluster in the green "tend to outperform" segment, when plotted Q is plotted against M. We already know that the QM combination is at, or near the top for the various Stocko factor combinations since their inception in 2013, so for me a high probability that Peaceful Life is likely to perform well.

A Quick Look at the best targets to use for QVM Ranks for different risk appetites - is bigger always better?

Introduction

50% quantile yearly returns

Unlock the rest of this article with a 14 day trial

About the Author

Nick Ray

8 comments

Unlock the metrics for all these stocks and more...

Unlock the metrics for all these stocks and more...