Can you have too much of a good thing? How to screen out outliers.

13th Nov '18 by Nick Ray

12 comments 2915 reads

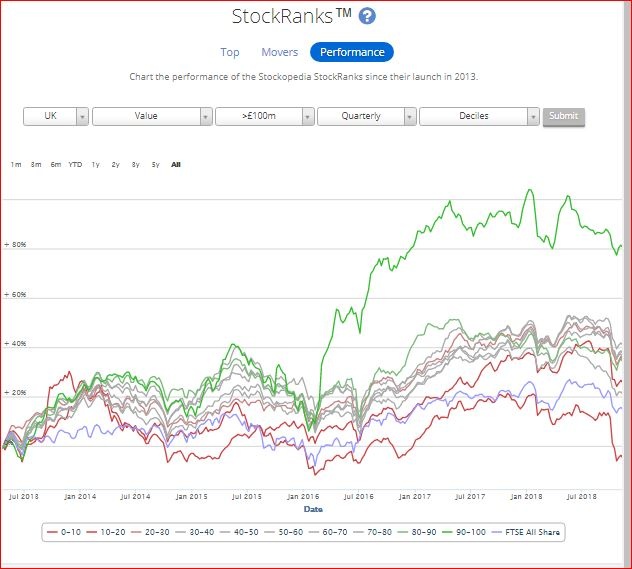
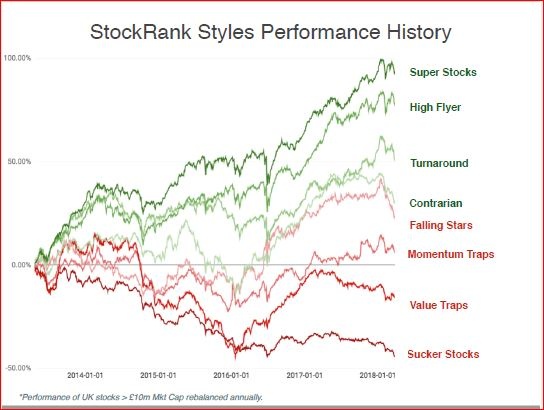
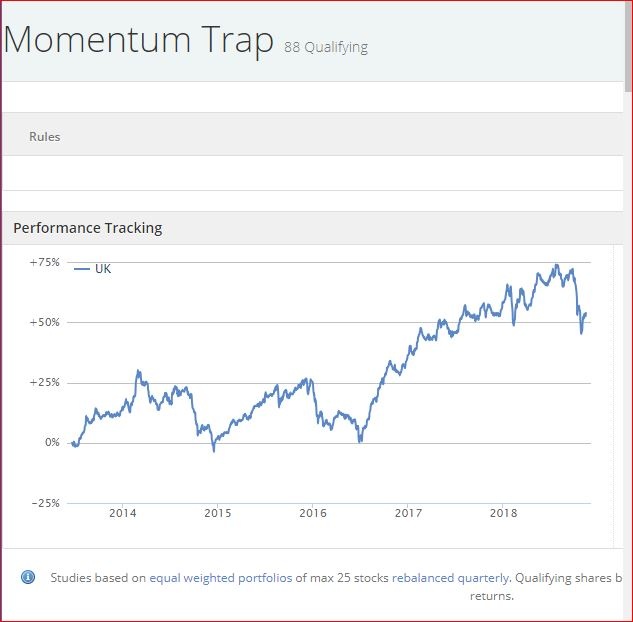
(Looking at the behaviour of stock fundamentals beyond two sigma.)

Motivation

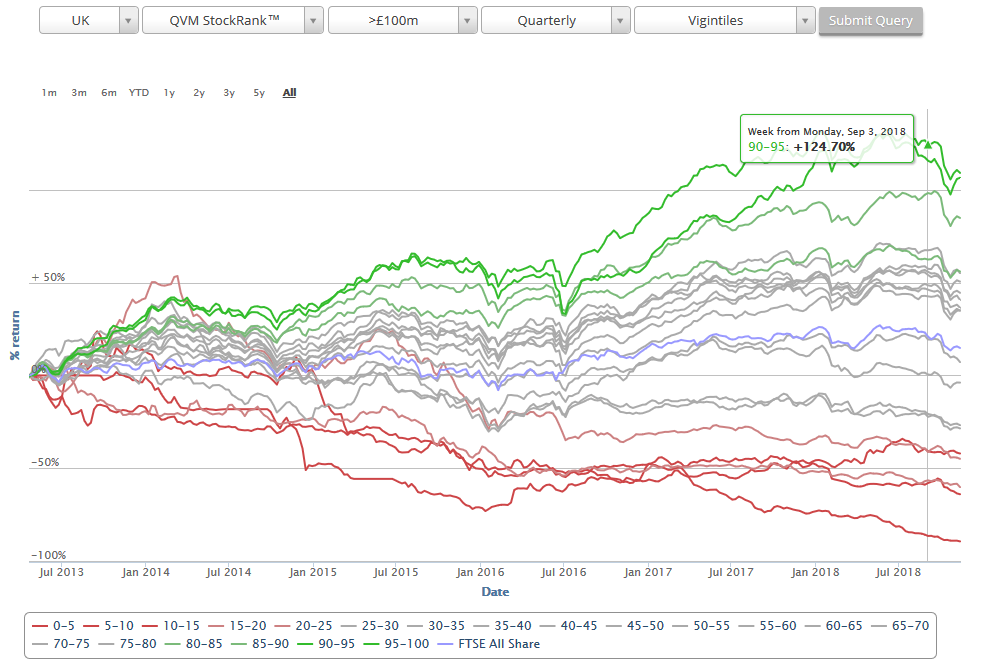
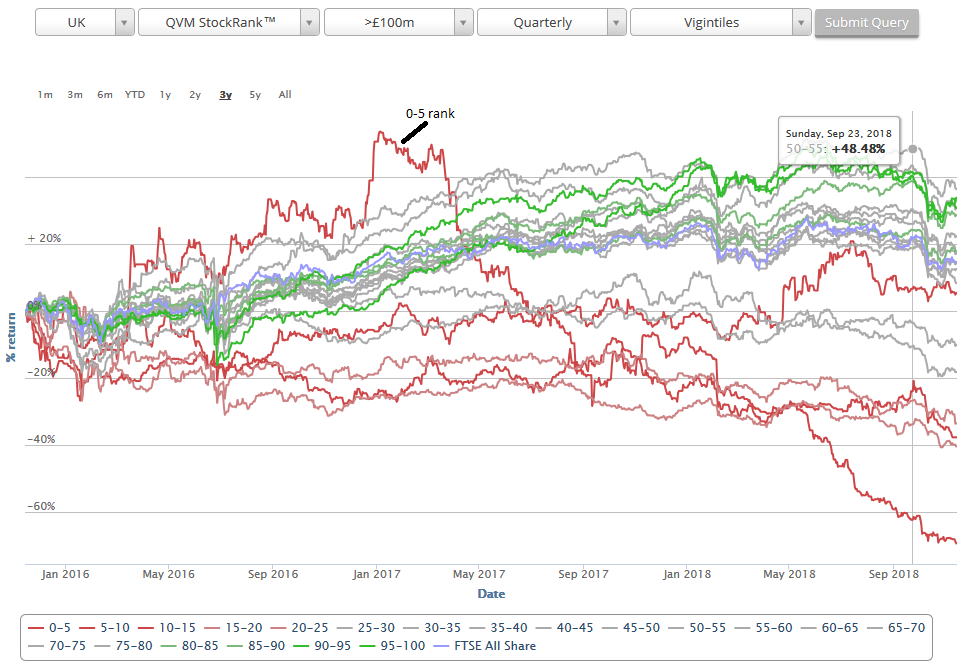
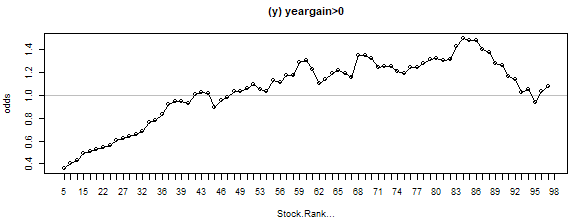
The genesis of this post was watching all the high-QM low-V stocks diving in the recent fall. All the backtest data says that you can't have too much quality or momentum when times are good. But how much is too much when things get a bit tricky?

Some time ago I wrote a post about the fat tails that you see on stock returns and discussed whether you could avoid the worst of the left fat tail.

Here is a quick summary of that post. We start with a histogram of log(stock returns) like this (where the sample data is in the grey blocks):

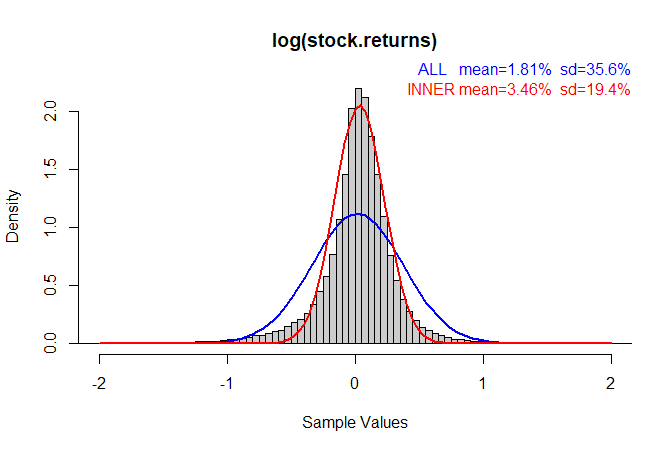
If I ask the computer to superimpose a "Normal" (Gaussian) distribution on the data I get the blue curve.

But something does not seem right here. The blue curve really does not follow the histogram's shape very well at all even though it was derived from the mean and standard deviation of the sample data.

The red curve seems to fit better near the middle of the histogram but it falls too quickly towards the tails which are "fatter". The red curve is generated by discarding the outliers before computing the mean and standard deviation first.

What this plot shows very clearly are the "fat tails" which Taleb talks about extensively in his books. The outlier stock returns happen more frequently than you would expect from a normal probability distribution. (Note: "Normal" here does not mean "normal" in the colloquial sense, but in the mathematical sense of a very specific probability distribution. It is called "normal" for interesting reasons.)

Let's look at a QQ plot of the data in the histogram. A "QQ" (quantile-quantile) plot is a plot where real sample data (in this case log(stock returns)) is placed in order and plotted against the same number of points taken from a theoretical distribution we want to compare the data against (in this case the Normal distribution.) The number labels on the X-axis are in "sigma", i.e. how many standard deviations from the mean the data is.

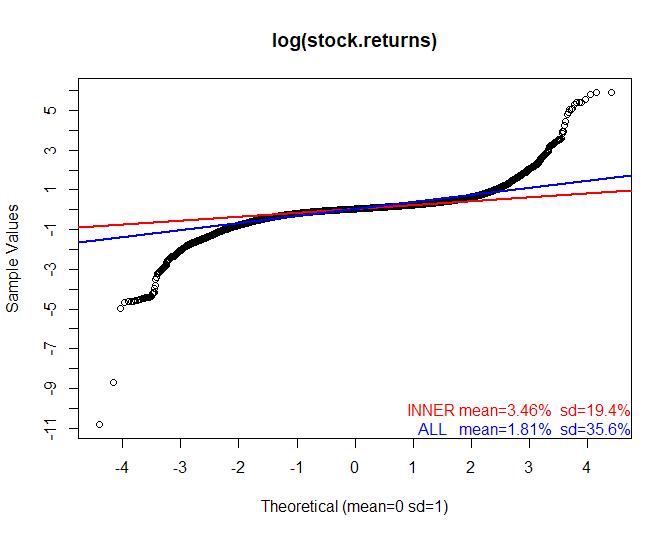
Any deviation from the theoretical distribution stands out very clearly as a deviation from a straight line. What we see is that the…

Unlock with Email

Unlock with Google

Already have an account?
Login here

Name

Value Rank

P/S

Serica Energy (LON:SQZ)

31.3

Versarien (LON:VRS)

22.2

WANdisco (LON:WAND)

14.4

Frontera Resources (LON:FRR)

40.9

Learning Technologies (LON:LTG)

12.4

Beeks Financial Cloud (LON:BKS)

11.3

Ideagen (LON:IDEA)

8.83

Craneware (LON:CRW)

17.1

Name

Value Rank

P/S

Oxford Biodynamics (LON:OBD)

153

Nanoco (LON:NANO)

37.2

Angle (LON:AGL)

104

Aquis Exchange (LON:AQX)

48.7

Angus Energy (LON:ANGS)

2841

European Metals Holdings (LON:EMH)

167

IronRidge Resources (LON:IRR)

2226

underscored

13th Nov '18

Oh, that's nice. I chased the High QMs low Vs through the last 2 years, and selected for the extremes! Some serious money seemed to be doing it too as they just kept going up parabolic-ally.

All of them got hit in this market correction. It will be interesting to see whether performance returns in that bucket or if that was a one off time period.

dfs12

14th Nov '18

I would imagine that excluding stocks with overly high V ranks would definitely make sense. But i imagine that excluding a stock that has an overall stock rank of 100, where it is made up of a consistent blend of underlying ranks say all in he high 80s, would be mistake.

GrahamF

Great post Nick.

I had been wondering whether with the NAPS what we may be seeing is the outperformance of one or possibly two stocks saving the bacon of the portfolio overall and if so why is that? Would we not expect to see a more even spread of returns through the constituents of the NAPS but just the winners doing a little bit better than the losers?

Does your work on outliers lead to any thoughts about how outliers may be improving the performance of the NAPS? Just wondering if NAPS is being ‘lucky’ in having selected the odd outlier on the positive side and so the overall performance may be as a result of that rather than the NAPS system as such to an extent.

Taff6

Nick

Another great Post, Thank u. I’m just wondering if you’re being a little tight with your parameters though. As Stockopedia data suggest that value ranks below 10 i.e. the most expensive 10% in the market under perform the index. (Mkt Cap set to 100 M for your preference)

As you demonstrate though, by scrutinising this data you believe that it’s actually only 20% of this 10% that are predominately causing the under performance. However, from a screening point of view, don’t we need a little room for growth? Nonetheless I think if used in conjunction with Stockopedia stockrank style categories you may be onto a winner. There are four Winning Styles (Super Stocks, High Flyers, Contrarian and Turnaround) and four Losing Styles (Sucker Stock, Momentum Trap, Value Trap and Falling Star). With some stocks not fitting any style and these are classified as Neutral. Below is their collective performance when compared against each other.

If one added, excludes shares with V <10 and Momentum traps to one’s screening ratios of choice in order to avoid overpaying for shares and then considered using your findings as a sell trigger of sorts i.e. V rank <2 or V rank <2 in conjunction with Momentum trap = Sell, deploy stops or closely monitor for signs of weakness. This could possibly be very effective!

This is the performance of Momentum traps as defined by stockopedia

which doesn't look to bad for a loosing style. They've done very well since Brexit referendum BTW!

Any thoughts?

pka

This is an interesting article, but I don't agree with it's conclusion to avoid stocks with StockRanks greater than 98. The StockRanks are not calculated by assuming any particular underlying probability distribution, whether that's the normal distribution or another one. I think all they do is provide a simple way to rank stocks relative to each other based on a combination of factors that Stockopedia considers to be desirable for future out-performance relative to the market as a whole. So a stock with a rank of 100 is slightly 'better' in that sense than one of 98, which is 'better' than one of 90, and so on. I can't think of a good reason why one should avoid a stock with a rank of 100, just because the distribution of ranks does not fit the normal probability distribution particularly well.

Dickyfit

Similarly I found the article interesting but didn't quite get it. If you look at vigintile (lovely word :-) ) performance data for V, M or Q then the 95-100 rank group outperform all others. So if there is something bad and to be avoided about the 98-100 range then the 95-98 range must be super stella.

Actually I now think I was wrong when I wrote that the StockRanks are not calculated by assuming any particular underlying probability distribution. I now think they are calculated by assuming a uniform probability distribution between 0 and 100. But the point is that a uniform distribution is very different from a normal distribution, so I still think there is no reason to avoid stocks with ranks greater than 98.

Nick Ray

15th Nov '18

That is a very good point. It is probably still meaningful when blending ranks from a similar distribution (such as all from the same category) but it is not at all clear that that blending from very different distributions works. In particular I think Q and M are similar but V is very different.

This has sent me off-topic a bit this evening (!) trying to work out a different way to blend Q and V to see what kind of difference it makes to the results. If it comes to anything I'll make a new post to talk about it. (For those curious I am modelling it on the fact that the way to combine expected return with volatility is to compute return/volatility. So I am trying to simulate (shape of Q distribution)/(shape of V distribution). This has the effect of preferring mid-values for V which is something I've written about previously.)

I'm not entirely convinced that is true.

Here is the QVM report for all years. The 90-95 vigintile is the highest:

Here is the same data but limited to the last 3 years. The 50-55 vigintile is the highest. You can also see that the 0-5 vigintile was the "best" in Jan 2017 on the basis of this graph.

Now to be honest these graphs look pretty but they are not really usable for working out whether the rankings are truly working - for all sorts of reasons. But even on their own terms you can easily find cases where the ranks reverse for any of the "Rank" metrics (Q, V, M, SR) for significant periods of time. (You will also find periods where the top vigintile is on top of course.)

FWIW my attempt to compute how well Stock Rank performs looks like the graph below. The y-axis is in "odds" that a stock will return >0% over the next year for a given Stock Rank. (so odds=1 is a 50% chance.)

In my data the droop for SR actually starts quite a bit earlier than the high 90s so it is not really a part of the point in the article.

The effects I am discussing in the post are in the tails and the main reason to discard them is to reduce the volatility of the portfolio since my assertion is that stocks with extreme values for a performance metric are not going to behave in a predictable way in the next period.

Hi Taff6

My real concern was to shave off a tiny fraction of very high scoring stocks as "unreliable". So essentially saying "go with the highest performance you can get" except for the top one or two percent which are often a seriously long way away in terms of absolute performance from the next few stocks down in the rank.

I've confused the message quite a lot by mentioning V <= 2. In that case if I am pursuing a QM strategy and ignoring V, the argument is that V <= 2 is so far into the left tail that it starts to be concerning.

In other words, the stock isn't just expensive (OK) it is ridiculously expensive. It may only be one ranking point from V=3 to V=2 but compare the change in P/S for example.

Name	Value Rank	P/S
Serica Energy (LON:SQZ)	3	31.3
Versarien (LON:VRS)	3	22.2
WANdisco (LON:WAND)	3	14.4
Frontera Resources (LON:FRR)	3	40.9
Learning Technologies (LON:LTG)	3	12.4
Beeks Financial Cloud (LON:BKS)	3	11.3
Ideagen (LON:IDEA)	3	8.83
Craneware (LON:CRW)	3	17.1

Name	Value Rank	P/S
Oxford Biodynamics (LON:OBD)	2	153
Nanoco (LON:NANO)	2	37.2
Angle (LON:AGL)	2	104
Aquis Exchange (LON:AQX)	2	48.7
Angus Energy (LON:ANGS)	2	2841
European Metals Holdings (LON:EMH)	2	167
IronRidge Resources (LON:IRR)	2	2226

Nick
Thanks for your reply, no confusion I think we were signing from the same hymn sheet just looking at it slightly differently. Many tangents to explore from this info though, thanks.

WarrantStar

18th Nov '18

I found the article very interesting, but remain unconvinced. I suspect that changes to the start & end dates of the analysis would probably produce very different results. This is likely to happen as a result of changes to the overall market sentiment eg between greed & fear, or whether it is growth stocks or value stocks which are in the ascendency.

Can you have too much of a good thing? How to screen out outliers.

Motivation

Unlock the rest of this article with a 14 day trial

About the Author

Nick Ray

12 comments

Unlock the metrics for all these stocks and more...

Unlock the metrics for all these stocks and more...